My daughter and I recently joined a scout sailing regatta. Lacking a real single-hander I sailed the kid’s Laser Bug while my daughter sailed her Sabot. However, since the Bug is a training boat generaly sailed in the UK, it doesn’t have an Australian Sailing yardstick. With a quick Google, I found a UK Portsmouth yardstick for it Aldeburgh Yacht Club - 1520 for the standard rig and 1440 for the race rig.

Using Portsmouth (PY) yardsticks:

\[Corrected \ Time = Elapsed \ Time × \frac{1000}{PY \ Number}\]

For Australian Sailing (AS) its:

\[Corrected \ Time = Elapsed \ Time × \frac{100}{AS \ yardstick}\]

So I just converted the 1440 to 144. However, the next day, thinking back on it, I realised there was no reason that should hold. What I should have done was to find some boats that had both PY and AS yardsticks, map the relationship between them and interpolate. A quick match up of the lists gave me 37 boats with yardsticks in both systems - with a pretty good linear relationship between them (the two obvious outliers are the RS600 and Hansa Liberty).

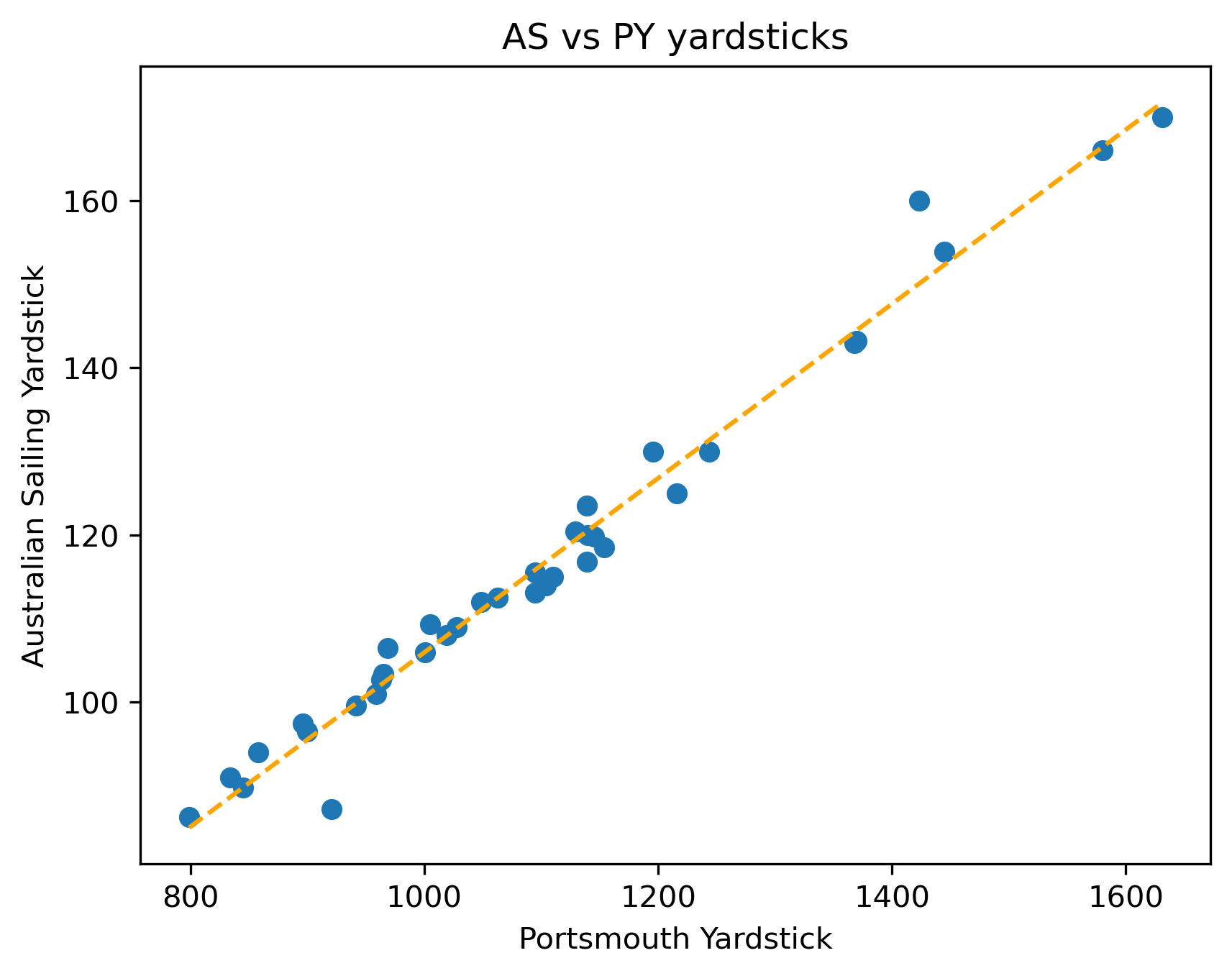
australian vs portsmouth yardsticks

The linear model gives a conversion formula of

\[AS = .1042×PY + 1.73\]

This results in an approximate AS yardstick of 152 for the Laser Bug in race mode and 160 in standard mode. At least I didn’t give myself an unfair advantage!